La transformation vers l'industrie 4.0 est devenue un
axe majeur d’amélioration de la performance industrielle dans de nombreux
secteurs. Elle est basée sur plusieurs concepts clés adossés à la
digitalisation, dont le Jumeau Numérique fait partie intégrante (Terkaj et al.,
2015). Parallèlement, la méthode Conwip est une méthode de pilotage de flux
reposant sur le maintien de l'en-cours constant, et destinée à améliorer la
performance opérationnelle des ateliers de fabrication (Spearman et al., 1990).
Elle est traditionnellement basée – comme la méthode kanban – sur l’usage de
tableaux d’étiquettes pour visualiser les en-cours.
L'objectif de cet article est de montrer dans quelles
mesures l’efficacité de la méthode Conwip de pilotage d’atelier peut être
augmentée par une digitalisation qui intègre un jumeau numérique calculant des
informations prévisionnelles pour anticiper les situations de pilotage à venir.
Pour cela, nous exposerons en premier lieu les
principales caractéristiques de la méthode Conwip, puis nous décrirons les
tableaux de suivi traditionnellement déployés en atelier pour piloter les flux
en Conwip. Nous présenterons ensuite le concept de Jumeau Numérique et ses
apports dans l’Industrie 4.0. Nous décrirons alors les bénéfices potentiels de
la digitalisation d’un tableau de pilotage Conwip, avec un focus particulier
sur les fonctionnalités engendrées par la présence d’un Jumeau Numérique
directement incorporé dans un tableau digital en atelier. Nous terminerons par
un retour d’expérience basé sur l’utilisation en conditions réelles de
plusieurs tableaux digitaux de pilotage de production en mode Conwip.
2. METHODE CONWIP
2.1 Principe de la méthode
La méthode Conwip (CONstant Work In Process) a été
théorisée au MIT (Massachusetts Institute of Technology) dans l’article
fondateur de Spearman et al. (1990).
Il s’agit d’une méthode de pilotage de flux de production
qui maintient l’en-cours constant, de façon à contrôler le délai de
fabrication.
Comme le Kanban (Bomy, 1994), elle se base
fondamentalement sur La loi de Little qui relie le niveau d'en-cours sur une
ligne, sa cadence de sortie et le délai de la ligne :
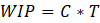 (1)
(1)
Avec :
WIP : en cours sur une ligne de fabrication en nombre de
produits,
C : cadence de sortie de la ligne en produits par heure,
T : délai de traversée de la ligne en heures.
Cette loi s'applique aussi bien aux lignes stables
qu’à celles qui possèdent une forte variabilité intrinsèque, en raison par
exemple de l’existence d’aléas sur les postes de fabrication, ou encore en
raison de durées opératoires variables pour les différents produits fabriqués.
L’application de cette loi montre que le contrôle du
niveau d’en-cours permet de maîtriser le délai de traversée.
Cette proposition n’est cependant vraie que si la
cadence reste inchangée. Or, trop réduire les en-cours peut mener à une baisse
de la cadence de sortie, en raison de ruptures d’alimentation momentanées en
pièces sur les postes de fabrication. Ce problème sera particulièrement aigu si
la ligne possède une forte variabilité intrinsèque. Le contrôle du niveau
d’en-cours consiste donc en premier lieu à viser un niveau suffisant pour
assurer la cadence de sortie souhaitée.
Sur une ligne de fabrication, la courbe qui donne la
cadence de sortie (par exemple en pièces par heures) en fonction de la quantité
d’en-cours chargés sur la ligne est du type suivant (Figure 1):
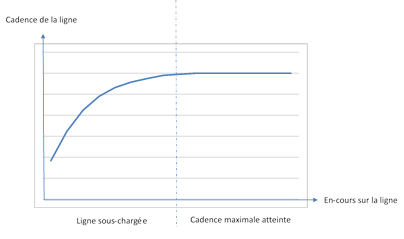
Figure 1 : Cadence d’une ligne vs En-cours
On voit qu’en deçà d’un certain niveau d’encours sur
la ligne, la cadence de sortie n’atteint pas son niveau maximum. En effet, les
postes goulets se désamorcent par manque de pièces, et la productivité de la
ligne décroît en conséquence. Cette première courbe incite donc à charger la
ligne avec un nombre de pièces élevé pour assurer la cadence de sortie
souhaitée.
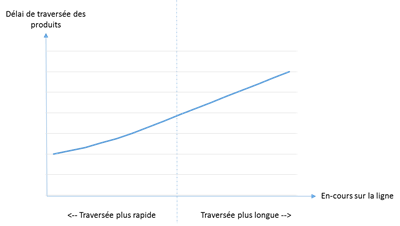
Figure
2 : Délai de traversée d’une ligne vs En-cours
Cependant, il est également nécessaire de considérer la courbe suivante, qui
donne cette fois le délai de traversée de la ligne par un ordre de fabrication,
toujours en fonction de la quantité d’en-cours chargés sur la ligne. Cette
seconde courbe découle directement de la loi de Little. Elle incite plutôt à
réduire l’en-cours pour viser des temps de réalisation courts :
<
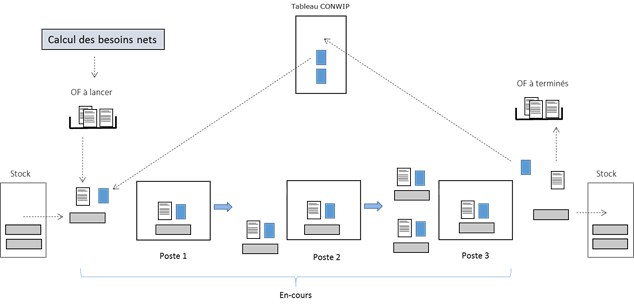
Figure 3 : Boucle Conwip
Lorsque l’on confronte ces deux courbes, on voit que l’idéal est bien sûr de
viser l’en-cours à la fois suffisant pour tenir la cadence de sortie voulue,
mais également limité afin de ne pas allonger au-delà du nécessaire les délais
de traversée. C’est pourtant le plus souvent dans la partie droite de ces
courbes que se trouve la majeure partie des systèmes de production pilotés en
flux poussé par la méthode Material Requirement Planning (MRP) (Baglin et al.,
2015). La cadence de sortie est assurée, mais l’en-cours est au-delà de ce qui
serait strictement nécessaire.
2.2 Fonctionnement d'une boucle Conwip
La méthode Conwip (CONstant Work In Process)
maintient constante la quantité d’en-cours présente à tout moment sur une ligne
de fabrication. Pour cela, elle utilise un nombre fixe d’autorisations à
produire, aussi appelées ticket Conwip. La consigne de pilotage est simple :
chaque ordre de fabrication envoyé en entrée sur la ligne doit être
obligatoirement accompagné d’une autorisation à produire. Lorsque toutes les
autorisations disponibles ont été engagées sur la ligne, les nouveaux ordres de
fabrication doivent attendre en début de ligne. Ainsi, la ligne ne sera pas
saturée par une quantité excessive d’en-cours. A l’autre bout, lorsqu’un ordre
de fabrication sort de la ligne, l’autorisation qui l’accompagne devient à
nouveau disponible. Cela permet alors l’entrée d’un nouvel ordre sur la ligne.
Le schéma suivant (Figure 3) décrit le principe d’une
ligne de fabrication pilotée en Conwip. Dans le cas présenté, les ordres de
fabrication sont émis par un système MRP à partir d’un processus de
planification et d’un calcul des besoins. MRP va ainsi indiquer quelle
référence doit être produite, et pour quelle date, ceci en fonction des
commandes clients fermes et/ou prévisionnelles. Le système Conwip prend ensuite
le relais de MRP au niveau de l’atelier afin de maintenir l’en-cours constant.
Les Ordres de Fabrication engagés sont représentés
sur des colonnes successives selon le principe de gamme-enveloppe de la ligne
(Jaegler, 2018). Une gamme-enveloppe est une suite d’opérations de fabrication
dans laquelle chaque référence qui passe sur la ligne va trouver son
cheminement en allant toujours de l’avant et en sautant éventuellement
certaines opérations. Cette représentation donne une très bonne visibilité sur
l’avancement des Ordres de Fabrication, sur les files d’attente à chaque poste,
et sur l’apparition éventuelle de goulets flottants sur la ligne.
3. JUMEAU NUMERIQUE
L’objectif premier de l’Industrie du Futur (Industrie
4.0 ou Smart Manufacturing) est de rendre plus intelligents les modes de
production grâce à la mise en réseau des machines et des hommes. Ainsi,
l’industrie 4.0 permet l’intégration sur trois axes de l’ensemble de la chaîne
de valeur (Shiyong et al. 2016) :
• l’intégration horizontale : tout au long de la chaîne de valeur,
les machines et les hommes communiquent en temps réel directement sur le centre
opérationnel ;
• l’intégration verticale : le pilotage des systèmes et des
sous-systèmes à travers la flexibilité et la reconfiguration des réseaux de
production ;
• l’intégration temporelle : tout au long du cycle de vie du
produit, les objets connectés enregistrent les données de conception, fabrication
et utilisation des produits.
Pour viser ces différentes intégrations, l’industrie
4.0 se base sur plusieurs concepts clés, dont le Jumeau Numérique qui est
considéré comme une virtualisation du monde physique, via une copie dans le
monde virtuel de données réelles collectées (Terkaj et al., 2015). Un Jumeau
Numérique est ainsi une représentation virtuelle d'un produit ou d'un processus
physique. Son objectif est d’appréhender le comportement de son équivalent
physique et de prédire son évolution dans le temps. Concernant la
représentation d’un processus manufacturier, le concept de Jumeau Numérique est
proche de celui de simulation. Toutefois, la différence réside dans le fait que
le Jumeau Numérique est connecté à la ligne réelle de fabrication.
Tao et al. (2018a) présentent le Jumeau Numérique
comme l’une des technologies les plus prometteuses pour la réalisation de la
fabrication intelligente et de l’Industrie 4.0. Ces auteurs ont publié en 2018
un état de l’art autour de cette technologie, ses composantes et son usage. En
utilisant les données fournies par des capteurs du monde réel, un Jumeau
Numérique est utilisé pour analyser et simuler le fonctionnement d’un système,
pour anticiper ses réponses aux changements, et pour en améliorer la performance.
Les Jumeaux Numériques font désormais partie
intégrante de la simulation, des tests et de l’exploitation de données massives
fournies par les objets intelligents (Tao et al., 2018b). Cette technologie
présente un fort potentiel pour la représentation, l’étude et l’analyse de
systèmes complexes, en particulier les systèmes logistiques (Guerreiro et al.,
2019).
Dans les cas que nous étudions, le Jumeau Numérique
va compléter le pilotage opérationnel quotidien sur un Conwip digital, en
donnant des informations prévisionnelles sur les situations de pilotage à venir
dans le futur.
4. Conwip Digital
4.1 Principes
Concrètement, digitaliser un tableau Conwip consiste
à transférer la version papier sur écran, sous forme de tickets numériques.
L’exemple qui suit montre le tableau Conwip digitalisé d’un atelier d’usinage,
avec sa salle d’attente à gauche et sa gamme-enveloppe en colonnes dans la
partie droite (Figure 7).
Le principe de la digitalisation d’un outil de
pilotage visuel est une pratique déjà largement testée en entreprise. Si l’on
met à part l’Echange de Données Informatisée (EDI) qui s’y apparente mais
concerne surtout la Supply chain externe, on trouve de premières descriptions
de digitalisations en 2008 par exemple dans (Lee‐Mortimer, 2008).
Cependant, Michel Greif (1989) avait décrit plusieurs
années auparavant les atouts concrets de solutions visuelles basées sur des
supports physiques et non pas informatiques, et exposé les risques de mauvaise
appropriation de solutions trop digitalisées. A sa suite, de nombreux auteurs
se sont interrogés sur les raisons du très faible nombre de cas d’adoption long
terme du Kanban digital (Lee‐Mortimer, 2008). Ces auteurs ont montré que
finalement les seules expériences qui durent sont celles où le Kanban digital
garde un mimétisme fort avec le Kanban physique, permettant ainsi aux
utilisateurs de manipuler au sens premier du terme des tickets digitaux sur des
écrans tactiles. Ces mêmes auteurs insistent sur le fait que l’intérêt des
entreprises pour le Kanban digital est finalement resté faible et que la
solution traditionnelle basée sur des cartes papier reste majoritairement
utilisée.
Concernant le Conwip, la digitalisation d’un tableau
papier en est à ses débuts. Le principe consiste à représenter sous forme
digitale les Ordres de Fabrication aux différentes étapes d’avancement, en
imposant un en-cours constant c’est-à-dire en imposant un nombre de jetons
Conwip virtuels limités.
Les retours d’expériences tirées des expérimentations
du Kanban digital montrent bien qu’il faut conserver ce mimétisme fort avec le
tableau papier, et permettre une manipulation tactile du ticket virtuel
identique au déplacement physique d’un ticket Conwip. Mais pour assurer
l’acceptation sur le terrain de la solution informatisée, il nous semble aussi
nécessaire que les tableaux digitaux apportent des fonctionnalités
supplémentaires qui ne sont pas réalisables en mode papier traditionnel.
Ces fonctionnalités supplémentaires sont :
•
La synchronisation avec l’ERP ou le MES
(Manufacturing Execution System), par création et avancement automatique des
tickets via un import régulier de données.
• La réplication du tableau Conwip en des lieux multiples lorsque
le périmètre de l’atelier est vaste.
•
La capitalisation de données de terrain permettant
de livrer des indicateurs de performance comme une Value Stream Mapping par
exemple.
• La prédiction de comportement de la ligne par calcul et
simulation sur un Jumeau Numérique.
Nous nous attachons par la suite aux fonctionnalités
apportées par le Jumeau Numérique.
4.2 Apports du Jumeau Numérique
4.2.1
Pronostics sur les dates de sortie des ordres de
fabrication MRP
Dans un système MRP, le calcul des besoins nets est
basé sur les délais d’obtention qui ont été paramétrés pour chaque article. Ce
sont des paramètres fixes alors que les délais réels d’atelier sont des
variables aléatoires qui dépendent fortement du niveau des files d’attente
devant chaque poste de travail.
Comme un système Conwip est capable de piloter des
références très différentes en termes de trajectoires de gammes, les délais de
traversée spécifiques de chaque OF sont très difficiles à pronostiquer.
Dans ce contexte, le Jumeau Numérique apporte une
solution de calcul intéressante. Il s’agit de faire vieillir l’atelier en
simulant l’avancement dans le futur de ses ordres de fabrication. La détection
de l’instant de passage simulé en fin de dernière opération donne pour chaque
Ordre de Fabrication engagé un pronostic sur sa date de sortie de ligne. Cette
simulation est basée sur la gamme individuelle de chaque OF et sur les
capacités des postes de fabrication. Le résultat du calcul dépend des files
d’attente que l’OF trouvera sur son passage, et éventuellement de son niveau de
priorité par rapport aux autres OF.
Ce calcul est réalisé à capacité finie et tient
compte de la situation réelle de l’atelier en termes de files d’attente. Il est
ainsi d’une meilleure précision que les délais standards paramétrés et utilisés
par MRP. Ce délai calculé peut être remonté régulièrement dans l’ERP pour
évaluer les écarts avec la date de fin d’OF planifiée.
Il est également possible de tester avec le Jumeau
Numérique l’impact sur les délais de la priorisation d’ordres de fabrication et
de l’ordonnancement de files d’attente. Un couplage optimisation-simulation
permet de rechercher par heuristiques des solutions d’ordonnancement minimisant
les écarts entre dates de fin de fabrication calculées et dates de fin de
fabrication attendues.
Dans un système Conwip, le pilotage s’effectue à
partir de la visualisation des files d’attente des différentes colonnes de la
gamme enveloppe : lorsque le niveau d’une colonne dépasse sa zone verte de
fonctionnement nominal, les capacités de ses ressources doivent être
augmentées.
Ce principe guide l’allocation du personnel
polyvalent sur la ligne : une personne apte à réaliser des tâches sur différentes
colonnes sera affectée aux colonnes dont la file d’attente atteint le niveau
rouge de façon à rééquilibrer en permanence la ligne.
En conséquence, on voit qu’il n’est pas nécessaire de
construire un planning prévisionnel pour chaque personnel de la ligne lorsque
l’on pilote un atelier Conwip. Le planning est le résultat de l’allocation
dynamique du personnel sur les postes des différentes colonnes du Conwip, en
fonction des goulots flottants constatés en temps réel.
Cependant, il reste utile de visualiser le diagramme
de Gantt des trajectoires des OF dans le futur. Le Jumeau Numérique permet de
construire ce diagramme comme résultat de la simulation de l’avancement des
différentes tâches sur les colonnes successives du tableau Conwip. La figure suivante
donne un exemple de planning prévisionnel reconstruit en temps réel par le
Jumeau Numérique à chaque mouvement de ticket virtuel sur le tableau digital.
Les étapes en jaune indiquent l’historique de la trajectoire de l’OF et les
étapes en mauve montrent le futur calculé.
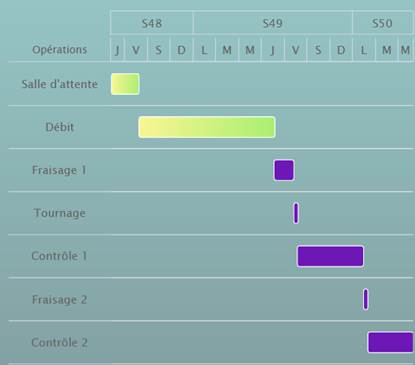
Figure 8 : Planning prévisionnel par simulation
4.2.3
Calcul de la charge prévisionnelle au poste de
travail
Un dernier apport du Jumeau Numérique est de prévoir,
toujours par simulation et à capacité finie, les zones futures de surcharge de
la ligne de fabrication.
La figure suivante est un exemple de thermographie de
charge future :
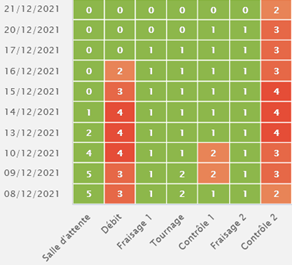
Figure 9 : Thermographie de charge future
Les colonnes de la gamme enveloppe du Conwip sont en
abscisse. Le temps se déroule sur l’axe des ordonnées, de bas en haut.
Les valeurs dans les cases indiquent le niveau prédit
des files d’attente des différents postes de fabrication dans le futur. La
couleur est calculée en comparant lors de la simulation sur le Jumeau Numérique
la taille des files d’attente atteinte chaque jour avec les indicateurs du
pilotage visuel.
Ce type de diagramme prévisionnel est utilisé pour
anticiper les pics de charge et planifier en conséquence les ajustements de
capacité.
5. Etude de cas
5.1 Contexte de l’étude
Nous présentons un retour d’expérience basé sur
l’utilisation de 14 tableaux Conwip numériques répartis sur les secteurs
suivants :
•
4 en fabrication mécanique traditionnelle,
•
3 en fabrication de cartes électroniques,
•
3 en réparation de produits industriels,
•
2 en horlogerie de précision,
•
1 en fabrication additive,
•
1 en certification de pièces industrielles.
Sur l’ensemble de ces cas étudiés, les processus de
fabrication ou de réparation étaient caractérisés par une forte
variabilité : soit par la diversité des références à fabriquer, soit par
l’instabilité du mix produit, soit par l’imprévisibilité des séquences en
entrée (cas de la réparation par exemple). Dans tous les cas, le Conwip a été
mis en œuvre pour réduire les en-cours, ainsi que pour mieux maîtriser et
prévoir les délais. Les autres méthodes de pilotage destinées à tendre les flux
(takt time, Kanban, Kanban d’emplacement) n’étaient pas mobilisables en raison
de la trop forte diversité des produits et de l’instabilité de la demande.
Dans sept de ces cas, le tableau digital a été
déployé à la suite d’une première phase d’expérimentation de la méthode de flux
tiré Conwip sous forme de tableau manuel traditionnel. Dans les autres cas, le
Conwip a été directement déployé en mode digital, mais ces ateliers étaient
déjà familiers de l’usage de tableaux de communication visuelle en atelier pour
la planification et le pilotage de la fabrication.
Le retour d’expérience présenté ici porte sur les
avantages et inconvénients d’une solution digitale 4.0 perçus par les
utilisateurs, avec un focus particulier sur les apports potentiels d’un Jumeau
Numérique.
5.2 Résultats du retour d’expérience
Les problèmes détectés sur une solution manuelle
traditionnelle de pilotage d’atelier ont été les suivants :
• Incohérence entre position des cartes sur le tableau et position
des en-cours,
• Interactions difficiles avec les périmètres éloignés de la zone de
localisation des tableaux Conwip,
• Difficulté du pronostic des dates de sortie des OF,
• Complexité de réalisation d’un planning d’atelier.
Les deux premiers points ont été améliorés par la
digitalisation des tickets, les deux derniers par les apports du Jumeau
Numérique.
5.2.1
Incohérence entre position des cartes et position
des en-cours
La première difficulté exprimée quant à l’usage d’un
tableau de pilotage d’atelier traditionnel est le possible décalage entre la
position des cartes sur le tableau et la position des OF dans l’atelier. Les
cartes doivent être déplacées manuellement à chaque fin d’opération de la gamme
de l’OF. En réalité le taux de complétude constaté est en moyenne de l’ordre de
80 %, ce qui signifie qu’une carte sur cinq n’est pas à sa bonne position sur
le tableau. Des procédures sont alors mises en place pour recaler régulièrement
les cartes mal positionnées, soit au moment de l’animation quotidienne
d’atelier devant le tableau, soit en amont par inventaire permanent des OF.
La digitalisation du tableau palie ce problème, à la
condition que le déplacement des cartes soit synchronisé automatiquement sur
les déclarations de fabrication réalisées dans l’ERP ou dans le MES. Dans ce
cas, et sous réserve d’une saisie rigoureuse de l’avancement dans l’ERP/MES, le
tableau digital reflète correctement et en permanence l’avancement des OF.
L’inconvénient constaté sur le terrain est que les utilisateurs interagissent
moins avec le tableau de pilotage, avec le risque d’une mauvaise appropriation
de la solution comme cela s’était produit pour le Kanban digital.
5.2.2
Interactions difficiles avec les périmètres
éloignés de la zone de pilotage des tableaux Conwip
Une seconde difficulté relevée lors de l’observation
des cas est la barrière à l’usage d’un tableau traditionnel pour les personnes
dont le poste de travail en est physiquement éloigné. Cela arrive lorsque le
périmètre de l’atelier est vaste, ou encore lorsque le processus de fabrication
incorpore des étapes particulières comme du traitement thermique ou du
traitement de surface. Le déplacement physique vers le tableau devient alors un
obstacle à la mise à jour des étiquettes.
Comme pour le Kanban digital entre client et
fournisseur, la digitalisation d’un Conwip apporte une solution par la
réplication possible du même tableau Conwip sur différents écrans répartis dans
l’atelier. Cette solution fonctionne en termes de saisie distribuée des
informations. Elle a toutefois l’inconvénient de renforcer l’isolement entre
les différents utilisateurs. Pour compenser ce problème, les utilisateurs de
solutions digitales répliquées imposent un temps quotidien de coordination de
l’équipe devant le même écran sous forme de routines d’animation. Cette
pratique est destinée à reconstruire la compréhension par tous de l’ensemble du
flux, afin de favoriser l’implication de chacun dans la performance globale de
l’atelier.
5.2.3
Difficulté du pronostic des dates de sortie des OF
Grâce à son en-cours constant, un pilotage en Conwip
assure à cadence fixe et via la loi de Little un temps de traversée moyen
constant. Toutefois, ce temps de traversée n’est qu’une moyenne sur l’ensemble
des OF. Sur tous les cas étudiés, les trajectoires des gammes varient beaucoup
d’une référence à une autre. En conséquence la dispersion des temps de
traversée autour de la moyenne y est trop forte pour baser un pronostic de
délai par OF sur cette seule moyenne. Avant digitalisation, l’estimation de la
date de sortie à partir d’un tableau Conwip traditionnel ou bien à partir d’un
planning d’atelier manuel était très difficile, car le temps de traversée d’un
OF dépend des files d’attente que l’OF verra devant lui quand il arrivera à
chaque poste. Quand chaque OF qui se trouve devant lui a une trajectoire de
gamme différente, la prédiction à la main par le planificateur est chronophage
et imprécise.
Le Jumeau Numérique embarqué dans le tableau
digitalisé a apporté dans l’ensemble de cas analysés une aide efficace à la
prédiction de délai de sortie de la ligne : suppression du temps passé par
le planificateur pour calculer les délais (cela prenait jusqu’à un jour par
semaine dans un cas particulier de l’échantillon observé) et amélioration du
niveau de précision des dates de sortie prévisionnelles de chaque OF.
5.2.4
Complexité de réalisation d’un planning d’atelier
Le planning d’atelier, souvent réalisé à l’avance
pour une semaine complète, est à la fois un outil d’allocation des tâches et de
vérification de la réalisation dans les temps du travail donné. Il indique le
travail à faire et la date à laquelle ce travail doit être terminé. En contexte
de variabilité, la construction d’un planning est complexe. Les évolutions du
mix produit empêchent de reproduire des motifs de planification à l’identique
d’une semaine sur l’autre. Mais surtout, une petite perturbation en début de
semaine peut générer des décalages sur l’ensemble des tâches en aval.
Passer en pilotage de type Conwip implique d’arrêter
de construire un planning puisque l’allocation des tâches est réalisée au fil
de l’eau en fonction du niveau des files d’attente et des OF prioritaires.
C’est d’ailleurs aussi le cas en Kanban, où la décision d’engagement d’un OF
résulte de l’atteinte d’un seuil sur la colonne du tableau.
La différence toutefois entre un Kanban et un Conwip
est que le Conwip s’applique à plusieurs opérations successives d’une gamme de
fabrication, mobilisant plusieurs ressources consécutives. Pour cette raison,
il est légitime de vouloir conserver la vision prospective donnée par un
planning, de façon à anticiper l’arrivée des OF sur un poste dans le futur
(préparation d’un outillage, organisation du poste, identification à l’avance
d’une personne qualifiée pour la référence à fabriquer …).
Comme indiqué plus haut, cette fonctionnalité de
calcul du planning prévisionnel des Ordres de Fabrication est apportée par le
Jumeau Numérique.
Le diagramme de Gantt est calculé automatiquement en
fonction des gammes, des files d’attente et de la dernière position réelle
connue des OF. Le planning d’atelier obtenu est ainsi utilisé comme donnée de
sortie de la planification et non plus comme donnée d’entrée. C’est dans la
pratique un outil de la digitalisation très consulté sur le terrain. Il apporte
de la profondeur d’analyse pour le responsable de secteur. Il lui permet
également de retrouver un mode de représentation habituel, favorisant ainsi la
transition vers l’usage du tableau digital.
6. CONCLUSIon
La digitalisation des tableaux de pilotage d’atelier
est une évolution logique qui s’inscrit totalement dans la transition actuelle
vers l’Usine du Futur. Elle apporte de nombreux atouts comme la création et
l’avancement automatique des tickets et la réplication des informations en
différents lieux de l’atelier.
Toutefois, pour en assurer la bonne appropriation sur
le terrain, il faudra dépasser la simple virtualisation d’étiquettes physiques
et mettre à disposition de nouvelles fonctionnalités augmentées pour le
pilotage d’atelier.
Le Jumeau Numérique est au premier rang de ces
fonctionnalités, à la condition qu’il soit mis directement à la disposition des
utilisateurs de terrain. Il permettra ainsi une prise de décision autonome au
plus près du flux de production, seule solution efficace pour gérer les
incertitudes permanentes qui caractérisent la fabrication en contexte de forte
variabilité.
7. REMECIEMENTS
Nous tenons à remercier Monsieur Philippe Dresin,
Directeur d’Exploitation LEON VEYRET et Directeur Performance Industrielle du
Groupe SAPIENS pour son autorisation d’utiliser dans cet article une
photographie du tableau Conwip d’un de ses ateliers.
8. REFERENCES
Baglin, G., Lamouri, S.,
Thomas A., (2015), Maîtriser les progiciels ERP. Editions Economica.
Bironneau , L. (2002).
Proposition d’un modèle d’aide au choix des méthodes et des outils de pilotage
de la production en milieu industriel. Revue Française De Gestion Industrielle,
21(1), 29–53. https://doi.org/10.53102/2002.21.01.419
Bomy, J.-M. (1994). Le
JAT et le Pilotage en flux tirés. Dimensionnement des boucles KABAN. Revue
Française De Gestion Industrielle, 13(1), 5–17. https://doi.org/10.53102/1994.13.01.216
Giard, V., & Mendy
Bilek, G. (2007). Production à flux tirés dans une chaîne logistique. Revue
Française De Gestion Industrielle, 26(1), 87–109. https://doi.org/10.53102/2007.26.01.679
Greif, M., (1989),
L'usine s'affiche : La communication visuelle au service du progrès, Editions
d’organisation.
Jaegler, Y.,
Jaegler, A., Burlat, P., Lamouri, S., Trentesaux, D., (2018), The ConWip
production control system: a systematic review and
classification. International Journal of Production Research, vol. 56, no
17, 5736-5757. https://doi.org/10.1080/00207543.2017.1380325
Jonsson, P.,
Mattsson, S., (2002), The selection and application of material planning
methods, Production Planning & Control, 13:5, 438-450. https://doi.org/10.1080/09537280210142763
Reeva
Lederman & Robert B Johnston (2011) Decision support or support for
situated choice: lessons for system design from effective manual systems,
European Journal of Information Systems, 20:5, 510-528.
https://doi.org/10.1057/ejis.2011.11
Lee‐Mortimer,
A., (2008), A continuing lean journey: an electronic manufacturer's adopting of
Kanban, Assembly Automation, Vol. 28 No. 2, 103-112. https://doi.org/10.1108/01445150810863662
Plenert, G.,
(1999), Focusing material requirements planning (MRP) towards performance,
European Journal of Operational Research 119.1: 91-99. https://doi.org/10.1016/S0377-2217(98)00339-7
Shiyong, W.,
Jiafu, W., Li, D., Chunhua, Z., (2016), Implementing Smart Factory of Industrie
4.0: An Outlook, International Journal of Distributed Sensor Networks, 4: 1–10.
https://doi.org/10.1155/2016/3159805
Spearman, M.,
Woodruff, D., et Hopp, W., (1990), CONWIP: a pull alternative to Kanban,
International Journal of Production Research, vol. 28. https://doi.org/10.1080/00207549008942761
Tao, F.,
Zhang, H., Liu, A., Nee, A., (2018a), Digital Twin in Industry:
State-of-the-Art. IEEE Transactions on Industrial Informatics.
Tao, F.,
Cheng, J., Qi, Q., Zhang, M., Zhang, H., & Sui, F., (2018b), Digital
twin-driven product design, manufacturing and service with big data. Int J Adv
Manuf Technol 94, 3563–3576. https://doi.org/10.1007/s00170-017-0233-1
Terkaj, W.,
Tolio, T., Urgo, M., (2015), A Virtual Factory Approach for in Situ Simulation
to Support Production and Maintenance Planning., CIRP Annals, 64: 451–454.
9. BIOGRAPHIE
 Anne-Lise Dumoutier :
Anne-Lise Dumoutier :
Docteure
en Informatique. Sa thèse concernait le Génie Industriel appliqué à la
fabrication additive. Ingénieur de recherche chez Wipsim, son domaine porte sur
les approches d’optimisation via la simulation.
 Jérôme Lions :
Jérôme Lions :
Géographe
de formation, Jérôme Lions a longtemps évolué dans le secteur environnemental.
Il s’est ensuite dirigé vers les nouvelles technologies pour occuper maintenant
un poste d’ingénieur en développement logiciel chez Wipsim.
 Patrick Burlat :
Patrick Burlat :
Patrick Burlat est Ingénieur Centrale-Supelec,
Docteur en économie, Professeur et HDR en Génie Industriel. Il dirige
actuellement la société Wipsim spécialisée dans l’optimisation du pilotage
d’atelier.
Anne-Lise
Dumoutier, WIPSIM, annelise.dumoutier@wipsim.fr,
 https://orcid.org/0000-0003-1234-4970
https://orcid.org/0000-0003-1234-4970
1, Jérôme Lions2, Patrick
Burlat3