Résumé
L’industrie 4.0 est le résultat de la convergence entre
l’industrie et le numérique. L’industrie 4.0 repose sur une relation
homme-machine plus collaborative. Cette collaboration de type réseau est
caractérisée par une communication continue et instantanée entre les moyens de
productions et d’approvisionnement. Ce qui permet une surveillance continue
d’éventuelles dérives de performance du système physique de production.
Cependant, la qualité de cette nouvelle organisation en réseau des moyens de
production dépend de la qualité des conditions initiales du système physique de
production. Pour contribuer au diagnostic du système physique de production, ce
papier propose un modèle de référence d’audit des gammes de production.
Mots clés : audit et diagnostic, propriétés d’analyse,
système physique de production, visualisation des connaissances
Reference model for the analysis of
physical production system data for a diagnosis 4.0
Abstract
Industry 4.0 is the
result of the convergence between industry and digital technology. Industry 4.0
is based on a more collaborative man-machine relationship. This network
collaboration is characterized by a continuous and instantaneous communication
between the means of production and supply. This allows for continuous
monitoring of any deviations in performance of the physical production system.
However, the quality of this new networked organization of production means
depends on the quality of the initial conditions of the physical production
system. In order to contribute to the diagnosis of the physical production system,
this paper proposes a reference model for auditing production routings.
Keywords : audit and diagnosis, analysis properties, physical
production system, knowledge visualisation
1. INTRODUCTION
Un des défis de la 4e révolution industrielle intitulés
« industrie 4.0 » est de répondre à cette exigence de produit unique et
personnalisé tout en conservant des coûts équivalents à une production de masse
et cela, malgré les faibles volumes de production engendrés. La réponse 4.0 se
traduit en autres, par la connexion des besoins du client au système physique
de production via l’évolution des systèmes de décision et d’information vers
des systèmes cyber-physiques. Il est généralement admis que la performance de
ces systèmes évolués de décision et d’information est dépendante de la
performance du système physique de production (SPP) (Koren et al., 1998 ; Rouse
et al., 2003). Compte tenu des enjeux financiers (Mayr et al., 2018), il faut
pouvoir régulièrement diagnostiquer et le cas échéant reconcevoir le SPP.
Un SPP efficient, dit « Lean », permettra de concevoir
un système de décision et d’information efficient (Chanegrih & Creusier,
2015, Amoako-Gyampah et al, 2008 ; Singh & Sharma, 2006). A contrario,
la non-performance d’un SPP, dit « non-Lean » est difficilement compensable par
la performance du système de décision et d’information (Nicoletti, B.
2013 ; Olhager, 2013, Lyonnet & Messaoudene, 2012, Real, R. et al.,
2010).
La littérature scientifique dénombre depuis plusieurs
décennies un nombre important de travaux sur la conception de SPP. Ces travaux
proposent une décomposition séquentielle systématique du processus de
conception du SPP en quatre phases (Irani et al., 2000 ; Muther, 1973 ;
Phillips, 1997 ; Raoot et al., 1993 ; Singh & Sharma, 2006 ; Tompkins
et al, 2003) :
- Phase
1 : Audit et diagnostic de l’implantation du SPP,
- Phase
2 : Elaboration des agencements conceptuels du SPP,
- Phase
3 : Elaboration des agencements physiques du SPP,
- Phase
4 : Implémentation du SPP.
Les
travaux développés dans ce papier se positionnent au niveau de la Phase 1.
Celle-ci consiste à préciser la prise en compte ou la non-prise en compte des
principes organisationnels du lean manufacturing dans l’implantation actuelle.
Cette phase va permettre d’identifier les causes principales de pertes de
performance ainsi que des principes de solutions potentielles.
Généralement différents principes de solution
d’implantation potentielles sont analysés. La difficulté majeure est
essentiellement liée au nombre important de points de vue à considérer :
sécurité, formation, mouvement, transport, qualité produit, procédé, temps de
production, gammes de production, etc. Ces points de vue sont en grande partie
liés aux flux physiques des produits. Le flux physique des produits représente
l’élément fondateur du SPP et est étroitement lié à la performance du SPP
(Alfnes & Martinsen, 2006 ; Leone et al., 2002 ; Tompkins et al.,
2003). Le point de vue considéré dans ce papier est le point de vue du flux
physique des produits modélisé dans les gammes de production, c’est-à-dire les
déplacements des produits entre postes de charge, appelé par la suite : ‘le
flux des produits’.
Le type de gammes de production considérée dans ce
papier sont des gammes industrielles de production : multiproduits (plusieurs
centaines), multi-opérations (plusieurs milliers), multipostes de charge
(plusieurs dizaines) sans prise en compte de gammes alternatives. Aussi, les
relations entre postes de charge créées par le flux des produits sont
potentiellement complexes. Cela renvoie à la question de l’intelligibilité du
flux des produits.
Comprendre le flux des produits consiste à auditer les
gammes de production pour en extraire les propriétés. Par exemple, les éléments
de réponse aux quatre questions ci-après représentent des propriétés des gammes
à auditer :
1. Est-ce
que certains produits sont fabriqués suivant la même séquence d’opérations ?
2. Est-ce
que certains produits sont fabriqués sur les mêmes postes de charge ?
3. Y
a-t-il des postes de charge qui ont un nombre important d’échanges avec les
autres postes de charge ?
4. Y
a-t-il des postes de charge qui sont systématiquement utilisés en début ou en
fin de gamme ?
Si par exemple la réponse associée à la question 1 est «
oui », alors le flux des produits défini sur l’ensemble des postes de charge
suit une structure d'ordre. Dans ce cas, le principe de solution à analyser
lors du diagnostic de l’implantation correspond à une implantation de type «
Ligne ». Le principe technologique de mise en œuvre revient à ordonner
spatialement les postes selon l’ordre d’utilisation des postes de charge dans
les gammes.
La question de recherche posée dans ce papier concerne
la possibilité de créer un modèle de référence pour l’audit de gammes de
production complexe dans un contexte dit « lean».
La suite du papier est
structurée comme suit.
La section 3 décrit la méthode
de construction du modèle de référence.
La section 4 décrit les règles
d’instanciation du modèle de référence.
La section 5 décrit la
validation du modèle de référence.
La section 6 conclut ce papier.
2. REVUE DE LA LITTERATURE
Le processus d’audit des gammes et de diagnostic de
l’implantation est usuellement décomposé en 4 activités dans la littérature
scientifique et représenté par un actigramme IDEF0 (Figure
1).
Le processus d’audit des gammes de production (A1, A2,
A3) est décrit à l’aide de la taxonomie adaptée de Card et al. (1999) et Chi (2000).
Par souci de précision, un cas d’école illustre la description de la phase 1
(Activité A1 à A4).
A1. Transformation des données
La transformation des données reformate les gammes de
production (Tableau 1) en format plus adapté appelé table de données (Tableau 2). Les 2 tables de données usuelles sont : matrice (produits - postes de
charge), matrice (postes de charge - postes de charge) orientée ou non. Ces
tables de données représentent les informations à visualiser.
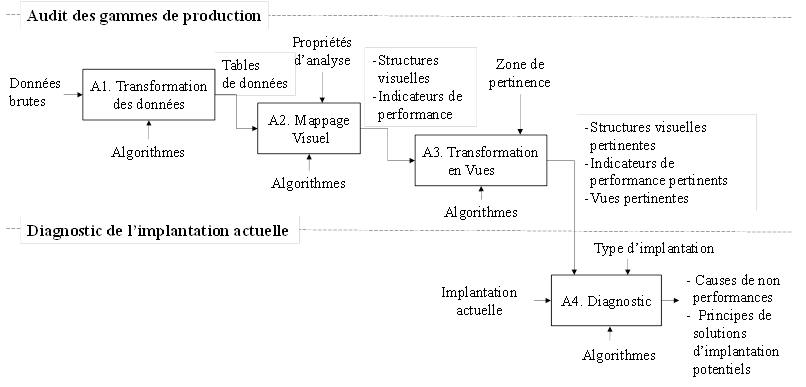
Figure 1. Phase 1 : audit des
gammes et diagnostic de l’implantation du SPP
Tableau
1. Données brutes
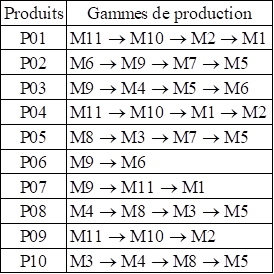
Nombre de Produits : 10
Tableau
2. Table de données
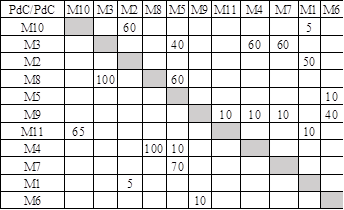
Nombre
de Postes de Charge : 11
A2. Mappage Visuel
Les mappages sont les
opérations d’analyse des tables de donnée. L’analyse consiste à décrire
visuellement les tables de donnée selon un ensemble de descripteurs, appelées
propriétés d’analyse par la suite. Pour chaque propriété d’analyse, des
algorithmes sont appliqués. Les résultats de ces analyses sont des structures
de données appelées structures visuelles et des valeurs d’indicateurs de
performance.
Par exemple et à partir des données du Tableau
2 une structure visuelle d’ordre est recherchée. L’algorithme permute les
lignes et les colonnes pour minimiser la quantité de flux sous la diagonale qui
modélise les flux de retour en arrière. L’indicateur de performance qualifie le
taux de flux de retour arrière. La structure visuelle obtenue est présentée
dans le Tableau 3.
Tableau 3.
Structure visuelle d’ordre

Indicateur de performance
Taux de flux de retour arrière pondéré = somme des
pondérations sous la diagonale / somme des pondérations totale.
= 75/785
» 9,6 %
A3. Transformation en Vues
Si une propriété d’analyse est jugée pertinente alors la
structure visuelle associée est transformée en vue par des algorithmes de
tracés de graphe orienté et pondéré.
Les sommets et arcs du graphe représentent
respectivement les postes de charge et les flux des produits entre postes de
charge. La Figure 2 représente la vue obtenue à partir de la structure visuelle
d’ordre du Tableau 3. La gamme fictive est définie par la succession de l’ensemble
des postes ordonnés suivant une structure d’ordre (Tableau 3, Rang (PdC)).

Figure 2. VUE : Relation
d’ordre total entre les postes de charge
La question 1 du questionnement d’audit ci-dessus est
reposée : est-ce que certains produits sont fabriqués suivant la même séquence
d’opérations ? Le taux de flux de retour arrière pondéré de 9,6 % est jugé
pertinent. La vue jugée pertinente en sortie de l’activité A3 permet au
concepteur par lecture visuelle d’observer la structure d’ordre. Cette vue est
une représentation qui est familière au concepteur et dans laquelle il lui est
aisé d’analyser en raison du lien physique avec le plan de l’implantation
actuelle (Figure 3).
A4. Diagnostic de l’implantation
Le diagnostic consiste à vérifier si l’implantation
actuelle correspond à un type d’implantation.
Dans cet exemple la structure d’ordre est jugée
pertinente. Le type d’implantation correspondant à la structure d’ordre est une
implantation de type ligne. Le dessin de la gamme fictive sur le plan
d’implantation (Figure 4) montre que les postes ne sont pas implantés en ligne.
Le dessin de la gamme fictive décrit de nombreux croisements et des flux de
retours en arrière, ce qui caractérise les causes de non-performance. Une
implantation en ligne représente un principe de solution d’implantation
potentiel pour la phase 2 d’élaboration d’un agencement conceptuel.
La vue (Figure 2) fait a priori apparaitre l’existence
de 2 classes distinctes de postes de charge (« Classe 1 : M9, M4, M8, M3, M7, M5, M6 » ;
« Classe 2 : M11, M10, M2, M1 »).
Sans le flux entre le poste de charge M9 et M11, les deux classes seraient
indépendantes.
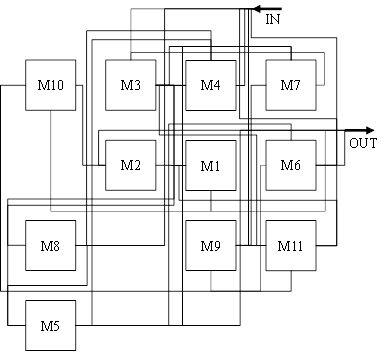
Figure 3. Plan de l’implantation
actuelle et flux des produits
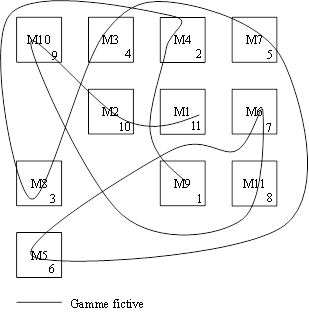
Figure 4. Représentation de la
gamme fictive sur le plan de l’implantation actuelle
La question 2 du questionnement d’audit ci-dessus est
reposée : est-ce que certains produits sont
fabriqués sur les mêmes postes de charge ? Deux structures
visuelles sont a priori combinées dans la vue, respectivement liées à la
propriété d’ordre et de classe.
Le processus d’audit des gammes de production et de
diagnostic de l’implantation du SPP (activités A1 à A4) peut être réitéré en
considérant la propriété d’analyse de classe.
Mener la phase 1 d’audit et de diagnostic de manière
intuitive comme ci-dessus peut s’avérer fastidieux et chronophage compte tenu
du type de gammes considérant plusieurs milliers d’opérations. Le caractère
fastidieux et chronophage ne permet pas de surveiller de manière continue
d’éventuelles dérives de performance du SPP.
Afin de contribuer à systématiser et accélérer la phase
1 (Figure 1) et plus précisément l’audit des gammes de production, deux
questions de recherche Q1 et Q2 sont posées :
Q1 : concernant l’activité A2 (Figure
1) quelles sont les propriétés d’analyse, les structures visuelles et
indicateurs de performance à appliquer aux tables de données ?
Q2 : concernant l’activité A3 (Figure
1) quel est l’ensemble des structures visuelles et combinaison de structures
visuelles potentielles à transformer en vues ?
La requête effectuée dans la littérature scientifique
est relative aux mots clés extraits des questions Q1 et Q2 : gammes de
production, propriétés, structures visuelles, indicateur de performance, vue.
Le Tableau 4 présente les propriétés d’analyse, les structures visuelles et les
indicateurs de performance recensés. Chaque propriété d’analyse est mise en
correspondance avec le type d’implantation et le principe technologique du type
d’implantation.
Les 7 types de relations Propriétés d’Analyse –
Structure Visuelle (PA-SV) recensés dans la littérature scientifique sont : 1.
ordre total, 2. ordre partiel, 3. niveau d’antériorité, 4. relation, 5. classe,
6. source, 7. puits. Pour chaque type de propriété d’analyse, un nombre
important d’algorithmes d’analyse sont proposés. Les types de propriétés
d’analyse les plus étudiés concernent principalement les types « classe
et ordre ». La classe regroupe en famille les postes de
charge ce qui permet lors de la phase d’élaboration des agencements
physique du SPP de tirer profit de la similarité des séquences des opérations
des différents produits pour diviser l’ensemble des postes de charge en unités
de production plus petites (type d’implantation : cellule) et ainsi simplifier
la gestion (De Guio et al., 1999). L’ordre permet de déterminer un
« sens » dominant de flux des produits entre les postes de
charge ; ce qui favorise la hiérarchisation des opérations suivant les
procédés (type d’implantation : ligne), et simplifie ainsi les flux (Zhou et
al., 1996).
Les algorithmes utilisés pour trouver des structures
visuelles à partir des propriétés d’analyse sont formalisés sous la forme de
problèmes d'optimisation combinatoire. Pour chaque problème plusieurs méthodes
d'optimisation sont proposées. Avec l’accroissement des vitesses de calcul
durant ces 30 dernières années, ces méthodes ont trouvé leur pleine
application. A titre d’illustration pour la propriété
d’analyse classe, la littérature dénombre plusieurs types
d’algorithmes comme : graph theorical methods (Rajagopalan, 1975),
array-based methods (King, 1980), mathematical programming based methods
(Kusiak, 1987 ; Srinivasan et al., 1990), search methods (Boctor, 1991),
neural network based methods (Kaparthi & Suresh, 1992), clustering methods
(Barth & De Guio, 1999 ; De Guio, 1999), incremental cell-formation method
(Mahesh & Srinivasan, 2002), Genetic Algorithm optimisation method (Hicks,
2005). Lee et al. (2004) ont développé 6 méthodes de recherche
heuristique basées sur les algorithmes ‘simulated annealing’ et ‘tabu search’.
Les algorithmes sont comparés par rapport au temps de
calcul de recherche de solutions optimales. Yin et Yasuda (2006) développent
une étude comparative des différents coefficients de similarité recensés dans
les algorithmiques de construction de classe. Ils dénombrent 17 coefficients de
similarité. Il propose une taxonomie pour mettre en correspondance les
différents coefficients de similarité.
Les travaux de la littérature étudient principalement
l’application d’une propriété d’analyse à la fois. Ils décrivent la structure
visuelle résultante et les indicateurs de performance associés.
Plus rarement, des travaux étudient l’application d’une
combinaison de structures visuelles. Par exemple, Lee (2004) propose l’étude de
l’application de la propriété d’analyse de niveau combinée avec les propriétés
d’analyse de « puits et source ». Cette combinaison permet par exemple de
regrouper les postes de charge de début de gammes de production (type
d’implantation : zone de lancement de production) et de fin de gammes de
production (type d’implantation : zone de fin de production) dans un niveau
donné et ainsi simplifier la gestion des lancements et des fins de production.
Les éléments ci-dessus permettent d’apporter une réponse
satisfaisante à la question Q1. Sept propriétés d’analyse, sept structures
visuelles, sept indicateurs de performance et six types d’implantation ont été
recensés dans les travaux de la littérature scientifique (Tableau 4).
Tableau
4. Synthèse des résultats de la requête bibliographique

Les éléments ci-dessus ne permettent pas d’apporter une
réponse complètement satisfaisante à la question Q2. Les combinaisons entre
structures visuelles sont très peu étudiées et explicitées. Pour mettre en
évidence la ou les propriétés dominantes ou distinctives des tables de données,
la juxtaposition des vues mono-structure visuelle ne suffit pas pour décrire
des vues multi- structures visuelles dues au fait de leurs combinaisons.
La prise en charge dans la vue de combinaisons de
structures visuelles a pour objet de faire émerger des caractéristiques
nouvelles (Card, 1999). Tenir compte simultanément des 7 relations PA-SV (Tableau 4) recensées revient à étudier un modèle générique de 127 structures
visuelles et combinaisons de structures visuelles (1).
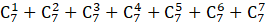 = 127 (1)
= 127 (1)
Il est difficilement concevable de mener 127 analyses
des tables de données à partir de 127 combinaisons de structures visuelles
transformées en 127 vues.
En résumé et à notre connaissance il n’existe pas de
modèle de référence pour l’audit des gammes de production
L’objectif de ce papier est de tester les potentialités
d’une démarche d’analyse combinatoire des structures visuelles selon les
principes organisationnels du lean manufacturing.
La contribution attendue est la création d’un
modèle de référence des structures visuelles et de leurs combinaisons
potentiellement pertinentes à transformer en vue. Ce modèle de référence doit
permettre l’automatisation de l’audit des gammes de production.
3. Conception du modèle de référence
Le modèle de référence est conçu en trois étapes (Figure 5).
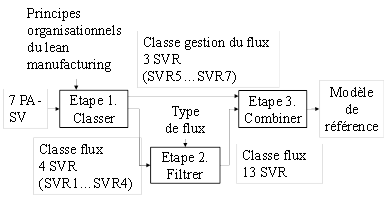
Figure 5. Conception du modèle du
référence (IDEF0)
3.1
ETAPE 1. Classer
La formalisation des principes technologiques des types
d’implantation associés aux propriétés (Tableau 4) permet d’identifier les deux
principes organisationnels du lean manufacturing lié au flux des produits :
principe 1. simplifier le flux des produits ; principe 2. simplifier la
gestion du flux des produits. L’étape 1 consiste à classer les structures
visuelles (Tableau 4) selon ces 2 principes indissociables, mais
conceptuellement distincts. Les 2 classes sont respectivement nommées :
classe flux (principe 1) et classe gestion du flux (principe 2). Les classes
flux et gestion du flux sont respectivement présentées dans le Tableau 5 et le Tableau 6. Les classes flux et gestion du flux comportent
respectivement 4 et 3 structures visuelles, appelées par la suite des
structures visuelles de référence (SVR).
Tableau
5. Classe flux

La classe flux doit prendre en compte la globalité du
flux des produits entre postes de charge (Burbidge, 1989 ; Tompkins et al.,
2003 ; Zhou et al., 2003). Ceci est essentiel puisque la phase
d’élaboration des agencements physique du SPP exige le positionnement de
l’ensemble des postes de charge sur la surface géométrique dédiée au SPP.
La classe gestion du flux doit permettre d’identifier et
de décrire des éléments de gestion du flux des produits relatifs à des postes
de charge. Ceci est essentiel puisque ces postes de charge requièrent un
positionnement et un type de gestion particulier dans l’implantation.
Concernant les propriétés source et le puits, deux types de gestion sont
distingués (Tableau 6) : une gestion centralisée et une gestion distribuée
respectivement pour les zones de lancement (type d’implantation 5.1 et 5.2) et
de fin de production (type d’implantation 6.1 et 6.2).
Tableau 6. Classe
gestion du flux

3.2
ETAPE 2. Filtrer
L’étape 2
consiste à filtrer les SVR de la classe flux selon les types de flux des
produits : flux de retour arrière, flux transitifs, flux direct
(Sarker et Xu, 2000). Ce
filtrage permet de mettre en évidence des connaissances par type de flux ou par
des combinaisons de types de flux. Les deux types de flux considérés pour le
filtrage sont : les flux transitifs et les flux de retour arrière. Sarker
et Xu (2000) qualifient ces deux types de flux : « compliquent le
flux », « perturbent le sens du flux ». Il n’est pas étonnant de
retrouver ces deux facteurs de bruit dans l’expression des indicateurs de
performance associés aux structures visuelles. Les 4 SVR de la classe flux sont
filtrées à l’aide de ces 2 types de déplacements. Après filtrage la classe flux
contient 13 SVR (Tableau 7) : 4 SVR (SVR1, SVR2, SVR3, SVR4) sans filtrage
et 9 SVR (SVR *.* avec filtrage).
3.3
ETAPE 3. Combiner
L’étape 3 consiste à combiner les 13 SVR de la classe
flux avec les 3 SVR de la classe gestion du flux. Il en résulte un modèle de
référence de 13 vues de référence (VUER)
(Tableau 7). La partie grisée indique les combinaisons de SVR à transformer en
vue.
A titre d’illustration, la VUER2 combine les structures visuelles suivantes : (classe
flux : ordre total acyclique) X (classe gestion du flux : source et
puits).
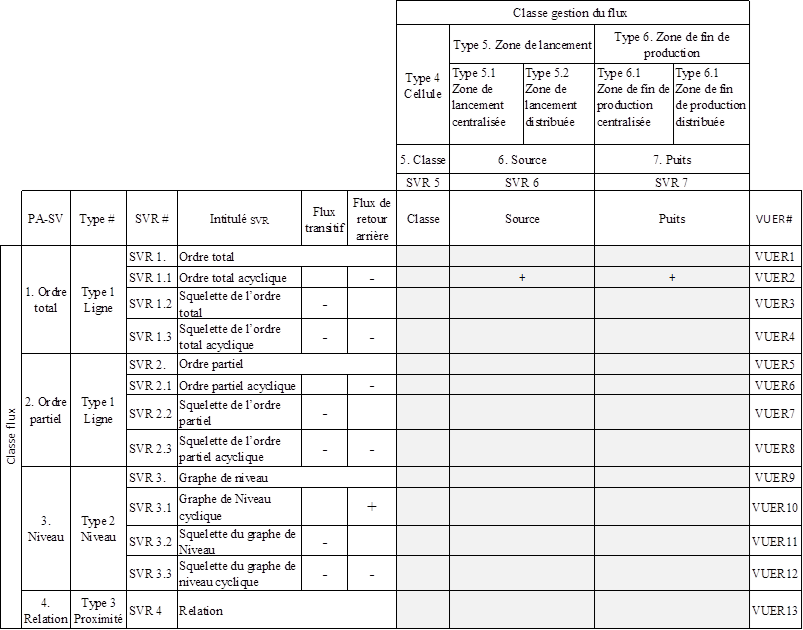
‘+’ visualiser ; ‘-‘
ne pas visualiser
4. INSTANCIATION DU MODELE DE REFERENCE
Cette section décrit la règle d’instanciation du modèle
de référence pour extraire un modèle particulier. Pour instancier le modèle de
référence, la règle suivante est appliquée : si la propriété
d’analyse est jugée pertinente, alors les structures visuelles associées sont à
transformer en vue (Figure 1, activité A3).
Notation :
j :
un indicateur de Performance
Vj :
valeur de j
VOj :
valeur optimale de j
Ij :
domaine de définition de j
Inf(Ij) :
valeur inférieure de Ij
Sup(Ij) :
valeur supérieure de Ij
Pj :
fonction de pertinence relative à j
qj :
seuil de pertinence de j
Zj :
zone de pertinence de j
Inf(Zj) :
valeur inférieure de Z de j
Sup(Zj) :
valeur supérieure de Z de j
dj :
distance entre VOj et Vj
Pour évaluer la pertinence des propriétés d’analyse, une
zone de pertinence Zj :[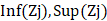 ] est définie pour
chaque indicateur de performance j (Tableau 4) relatif à chaque propriété
d’analyse. Cette zone de pertinence Zj est définie comme suit :
] est définie pour
chaque indicateur de performance j (Tableau 4) relatif à chaque propriété
d’analyse. Cette zone de pertinence Zj est définie comme suit :
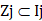 (2)
(2)
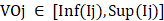 (3)
(3)
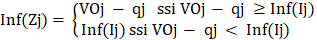 (4)
(4)
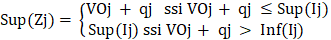 (5)
(5)
La définition du seuil de pertinence qj dépend
de plusieurs facteurs comme l’expérience du concepteur en charge de l’étude
d’implantation, le contexte de l’étude menée, le secteur d’activité, les
produits, les postes de charge.
Si la valeur de l’indicateur de performance Vj associée
à la propriété A est incluse dans la zone de pertinence Zj de A alors A est
jugée pertinente.
Pour savoir comment se situe la valeur de Vj par rapport
à VOj, on peut :
Définir dj comme suit : 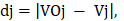 (6)
(6)
Et considérer la fonction Pj comme suit :
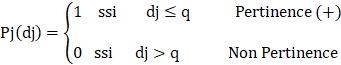 (7)
(7)
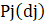 est une fonction de
[Inf(I), Sup(I)] sur {0,1}.
est une fonction de
[Inf(I), Sup(I)] sur {0,1}.
Le Tableau 8 précise pour chaque indicateur : la
formule, le domaine de définition (I) et la valeur optimale (VOj). Dans le cas
de la PA-SV source et puits, deux VOj sont précisés pour tenir compte des deux
types de gestion des flux centralisés et décentralisés.
Tableau 8. Indicateurs de performance,
formule, domaine de définition, valeur optimale

C : nombre de postes de charge ; F : somme
des flux entre postes de charge.
Les deux questions de validation du modèle de référence
sont les suivantes :
Q3 : Peut-on confirmer par l’expérimentation la
pertinence des propriétés d’analyse recensées dans la littérature scientifique
?
Q4 : Peut-on confirmer par l’expérimentation la
représentativité du modèle de référence ?
Pour répondre à ces questions, l’expérimentation
suivante est menée. Le processus d’audit des gammes de production (A1.
Transformation des données, A2. Mappage visuel, A3. Transformation en vues) est
appliqué sur 19 cas industriels. Afin d’opérationnaliser la validation du
modèle de référence, le processus d’audit des gammes est automatisé. L’objectif
est d’extraire automatiquement un modèle particulier relatif à chaque cas
industriel. À partir des données brutes d’un cas industriel particulier, les
résultats suivants sont générés : les structures visuelles, les indicateurs de
performance et l’affichage des vues pertinentes.
Les 19 cas industriels considérés sont issus des secteurs
d’activités de l’aéronautique, l’automobile et l’équipement électrique. Le Tableau 9 présente une description des 19 cas industriels (C1 à C19) à partir des
gammes industrielles de production (données brutes). Pour chaque cas, le nombre
de postes de charge, le nombre des produits et le nombre d’opérations sont
décrits.
Par souci de concision, seuls les résultats suivants
sont présentés : calcul des indicateurs de performances considérés (Tableau 10), calcul de la pertinence des propriétés d’analyse (Tableau
11).
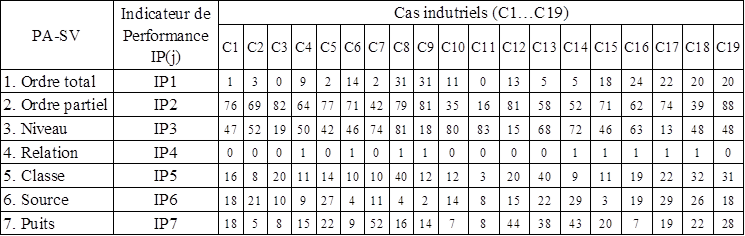
Le Tableau 10 présente les valeurs des indicateurs de
performance associés aux propriétés d’analyse. Les formules de calcul employées
sont issues du Tableau 8.
Le Tableau 11 présente pour chaque relation PA-SV, le
type d’implantation considéré, le seuil de pertinence, la zone de pertinence et
le résultat de calcul de pertinence.
Tableau
9. Description des 19 cas industriels (données brutes)
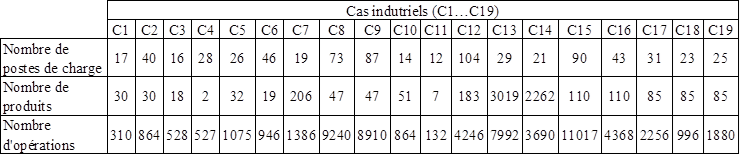
Tableau
10. Résultats de calcul des indicateurs de performance (Activité A2)
Tableau
11. Résultats de calcul de pertinence des propriétés d’analyse (Activité
A3)

Les résultats du Tableau 11 mettent en exergue les
observations suivantes :
Par ligne :
Aucune ligne n’est vide : chaque propriété d’analyse est
jugée pertinente au moins une fois.
Aucune ligne n’est complète : la pertinence des
propriétés d’analyse est contingente (Damand et al., 2021).
Par colonne :
Aucune colonne n’est vide : chaque cas industriel est
décrit par au moins une propriété de la classe flux et deux propriétés
d’analyse de la classe gestion de flux : classe flux (min=1) ; classe
gestion du flux (min=1).
Aucune colonne n’est complète : dans aucun cas, toutes
les propriétés d’analyses sont jugées pertinentes : classe flux
(max=3) ; classe gestion du flux (max=3).
Les observations ci-dessus sont liées à la fois à la
particularité des cas industriels étudiés et aux seuils de pertinence
considérés par propriétés d’analyse. Le seuil de pertinence qj est fixé pour
l’expérimentation à 20 % de la longueur du domaine de définition Ij pour toutes
les propriétés d’analyse. Ce seuil strict est aligné avec l’objectif de mettre en
évidence les propriétés dominantes et distinctives des tables de données.
Exemple du calcul du seuil de pertinence (q) et de la
zone de pertinence (Z) : pour l’IP1, (I:[0, 100[, V0j=0, q=20 (20 = 20 % 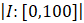 , Z:[0, 20]).
, Z:[0, 20]).
Les résultats représentent une capitalisation de
connaissances et non une signification statistique d’une population de cas
industriels. Le nombre de cas industriels est relatif. En effet, deux cas
suffisent pour montrer l’existence potentielle de la contingence des propriétés
d’analyse.
En réponse respectivement
aux questions Q3 et Q4 :
La pertinence des 7 propriétés d’analyse est confirmée.
Cependant, la pertinence des propriétés d’analyse est contingente.
La représentativité du modèle de référence est
confirmée. Chaque cas industriel a pu être caractérisé par des structures
visuelles de référence.
6. Conclusion
L’audit et le diagnostic
de l’implantation du SPP sont considérés dans ce papier. Le point de vue considéré est le point de vue du flux
physique des produits modélisé dans les gammes de production. Le processus
d’audit des gammes de production est usuellement décomposé en trois activités :
activité A1. transformation de données, activité A2. mappage visuel, activité
A3. transformation en vue.
Afin de mettre en œuvre
ce processus d’audit, 2 questions de recherche sont posées : (Q1) concernant
l’activité 2, quels sont les propriétés d’analyse, les structures visuelles et
indicateurs de performance à appliquer aux tables de données ? ; (Q2)
concernant l’activité 3, Figure 1, quel est l’ensemble des structures visuelles
et combinaisons de structures visuelles potentielles à transformer en vues ?
La revue de la littérature apporte une réponse acceptable
à Q1. Sept propriétés d’analyse, sept structures visuelles, sept indicateurs de
performance et six types d’implantation sont recensés. En revanche, la revue de
la littérature apporte une réponse incomplète à Q2. La contribution de ce
papier consiste alors à tester les potentialités d’un modèle de référence des
structures visuelles. La structuration du modèle de référence est basée sur une
taxonomie des structures visuelles selon 2 principes organisationnels du lean
manufacturing (simplification du flux des produits X simplification de la gestion
de flux du flux des produits). Le modèle de référence combine 13 structures
visuelles de référence liées au flux des produits avec 3 structures visuelles
de référence liées à la gestion du flux des produits. Le modèle de référence
compte 13 vues de référence.
La validation du modèle de référence soulève deux
questions : (Q3) Peut-on confirmer par l’expérimentation la pertinence des
propriétés d’analyse recensées dans la littérature scientifique ? (Q4) Peut-on
confirmer par l’expérimentation la représentativité du modèle de référence ?
L’expérimentation menée consiste à décliner le processus
d’audit des gammes dans le cadre de données brutes issues de 19 cas
industriels. L’expérimentation permet a priori de valider le modèle de
référence. D’une part, en réponse à Q3, les observations révèlent que la
pertinence des propriétés d’analyses est contingente. D’autre part, en réponse
à Q4, les observations révèlent que chacun des cas industriels est
caractérisé par des SVR. A noter que dans le cadre de l’expérimentation le
nombre de VUER varie entre 1 VUER et 8 VUER. Le nombre de VUER est corrélé avec
la valeur du seuil de pertinence des propriétés d’analyse. Moins le seuil de
pertinence est strict, et, plus le nombre de VUER est important avec un maximum
de 13 VUER. La compréhension du modèle de référence par le concepteur reste
cognitivement acceptable.
La perspective de ce travail concerne l’activité de
diagnostic du SPP (activité 4, Figure 1). L’implantation est-elle implantée
selon tel type d’implantation ? Quels sont les causes de
non-performance ? Quels sont les principes de solutions à
considérer ?
Afin d’intégrer le diagnostic 4.0 dans un système proactif
de surveillance des dérives de la performance du SPP, la contribution attendue
consiste à formaliser des indicateurs de mesure du degré de concordance entre
les propriétés contenues dans les gammes de production et les propriétés
contenues dans le plan d’implantation.
7. REMERCIEMENTS
Cette recherche est
réalisée dans le cadre du projet Offensive Sciences numéro 3.11 « Virtual
Innovative Real Time Factory » (VIRTFac) qui bénéficie du soutien
financier de l’Offensive Sciences de la Région Métropolitaine Trinationale du Rhin Supérieur, du programme INTERREG
V Rhin Supérieur et du Fonds européen de développement régional (FEDER) de
l’union européenne.
8. REFERENCES
Alfnes, E., & Martinsen, K.
(2006, July 25-28). Modeling and design of flow manufacturing systems for
SMEs [Paper presentation]. Proceedings of the 5th 3rd CIRP International
Seminar on Intelligent Computations in Manufacturing Engineering, Ischia,
Italy.
Amoako-Gyampah, K., &
Acquaah, M. (2008). Manufacturing Strategy, Competitive Strategy, and Firm
Performance: An Empirical Study in a Developing Economic Environment. International
Journal of Production Economics, 111(2), 575-92. https://doi.org/10.1016/j.ijpe.2007.02.030
Bard, J.F., & Feo T.A. (1989). Operations Sequencing in Discrete Parts
Manufacturing. Management Science, 35(2), 249-255. https://doi.org/10.1287/mnsc.35.2.249
Barth, M., & De Guio R. (1999). Industrial Implementation of Production Flow Analysis. In IRANI S.A.
(ed.) Handbook of Cellular Manufacturing
Systems, John Wiley & Sons., (pp. 497-527). https://doi.org/10.1002/9780470172476.ch16
Barth, M., De Guio R., & Zhou J. (1998,
August 9-12). A graph theoretic approach for the production
line formation problem. Proceeding of the 2nd
International Conference on Engineering Design and Automation, Maui, Hawaii.
Boctor,
F.F. (1991). A linear formulation of the machine-part cell formation problem. International Journal of Production Research, 29(2), 343–356. https://doi.org/10.1080/00207549108930075
Burbidge, J.L. (1989).
Production flow analysis for planning group technology. Journal of
Operations Management, 10(1), 5-27. https://doi.org/10.1016/0272-6963(91)90033-T
Card, S.K., Mackinlay, J.D.,
& Shneiderman, B. (1999). Readings in Information Visualization: Using
Vision to Think. San Francisco, California: Morgan-Kaufmann Publishers.
CHANEGRIH, T., & CREUSIER,
J. (2015). Le lean manufacturing dans l’industrie française : états des
lieux et implications pratiques. Revue Française De Gestion Industrielle,
34(4), 59–71. https://doi.org/10.53102/2015.34.04.831
Chi, E.H. (2000, October 9-10). Taxonomy of Visualization Techniques Using the Data State Reference
Model. Proceedings of the IEEE Symposium on Information
Visualization 2000. INFOVIS 2000, Salt Lake City, UT, USA. https://doi.org/10.1109/INFVIS.2000.885092
Damand, D., Gamoura, S., Barth, M., ‘Maturité du
système physique de production : modèle de diagnostic 4.0’, CIGI-Qualita21 :
Conférence Internationale Génie Industriel QUALITA- Grenoble, 5-7 mai 2021.
De Guio R., Barth, M. &
Zhou, J. (1996, July 9-12). Checking Algorithms for the Weighted Feedback
Arc Set problem with Order Constraints. Proceedings of the Symposium on
modelling, analysis and simulation: CESA'96 IMACS multiconference,
Computational engineering in systems applications, Lille, France.
De Guio, R., & Barth, M. (1999). Cell Formation Using Production Flow Analysis. In IRANI S.A. (ed.) Handbook of Cellular
Manufacturing Systems, John Wiley & Sons., (pp.
69-111). https://doi.org/10.1002/9780470172476.ch16
Deb, S.K. & Bhattacharyya,
B. (2002). Fuzzy decision support system for
manufacturing facilities layout planning. Decision Support Systems,
40(2), 305– 314. https://doi.org/10.1016/j.dss.2003.12.007
Frank, J. & Massey, J.R.
(1951). The Kolmogorov-Smirnov Test for Goodness of Fit. Journal of the
American Statistical Association, 46(253), 68-78. https://doi.org/10.1080/01621459.1951.10500769
Hicks,
C. (2004). A Genetic
Algorithm tool for designing manufacturing facilities in the capital goods
industry. International Journal of Production
Economics, 90(2), 199–211. https://doi.org/10.1016/S0925-5273(02)00467-X
Hollier, R.H. (1963). The layout
of Multi-Product Lines. International Journal of Production Research,
2(1), 47-57. https://doi.org/10.1080/00207546308947812
Huang, H. & Irani, S.A.
(2003, August 3-7). An enhanced systematic layout
planning process for high-variety low-volume (HVLV) manufacturing facilities. Proceedings of the
17th International Conference on Production Research, Blacksburg, Virginia.
Irani, S. A., Zhang, H., Zhou, J., Huang, H.,
Udai, T. K. & Subramanian, S. (2000). Production Flow Analysis and Simplification Toolkit (PFAST), International
Journal of Production Research, 38(8),
1855-1874. https://doi.org/10.1080/002075400188636
Kahn, A. B. (1962). Topological
sorting of large network. In: Communications of the ACM, 5(11), 558-562.https://doi.org/10.1145/368996.369025
Kaparthi, S., Suresh, N.C. &
Cerveny, R.P. (1993). An improved neural network leader algorithm for
part-machine grouping in group technology. European Journal of Operational
Research, 69(3), 342-356. https://doi.org/10.1016/0377-2217(93)90020-N
King, J.R. (1980).
Machine-component grouping in production flow analysis: an approach using a
rank order clustering algorithm. International Journal of Production
Research, 18(2),213–232. https://doi.org/10.1080/00207548008919662
Koren, Y., Hu J., & Weber T. (1998). Impact of Manufacturing System Configuration on
Performance. CIRP Annals, 47(1), 369-372. https://doi.org/10.1016/S0007-8506(07)62853-4
Kusiak, A. (1987). The
generalized group technology concept. International Journal of Production
Research, 25(4), 561–569. https://doi.org/10.1080/00207548708919861
Lee, D H., Kiritis, D., &
Xirouchakis, P. (2001). Search heuristics for operation sequencing in process
planning. International Journal of Production Research, 39(16), 3771-3788.
https://doi.org/10.1080/00207540110061922
Lee, D.H., Kiritsis, D., &
Xirouchakis, P. (2004). Iterative approach to operation selection and
sequencing in process planning. International Journal of Production Research.
42 (22), 4745-4766. https://doi.org/10.1080/00207540410001720412
Leone, G. & Rahn, R.D
(2002). Fundamentals of flow manufacturing. Flow publishing Inc. Boulder,
Colorado, USA.
Lyonnet, B., & Messaoudene, Z. (2012).
Relations entre les pratiques de management et le système lean opérationnel
d’entreprises françaises. Revue Française De Gestion Industrielle, 31(2),
63–82. https://doi.org/10.53102/2012.31.02.655
Mahesh, O. & Srinivasan, G. (2002)., Incremental cell formation considering alternative
machines. International Journal of Production
Research, 40 (14), 3291-3310. https://doi.org/10.1080/00207540210146189
Mayr, A.,
Weigelt, M., Kühl, A., Grimm, S., Erll, A., Potzel, M., & Franke, J.
(2018). Lean 4.0 - A conceptual conjunction of lean management and Industry
4.0. In Procedia CIRP, Volume 72 (pp. 622–628). Stockholm, Sweden. https://doi.org/10.1016/j.procir.2018.03.292
Muther, R. (1973). Systematic
Layout Planning. 2nd Edition, Cahners Books,
Boston.
Nicoletti B. (2013). Lean and
Automate Manufacturing and Logistics. In: Prabhu V., Taisch M., Kiritsis D.
(eds) Advances in Production Management Systems. Sustainable Production and
Service Supply Chains. APMS 2013. IFIP Advances in Information and
Communication Technology, vol 415. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-41263-9_34
Olhager, J. (2013). Evolution of
Operations Planning and Control: From Production to Supply Chains. International
Journal of Production Research, 51 (23–24), 6836–6843. https://doi.org/10.1080/00207543.2012.761363
Phillips, E.J. (1997). Manufacturing
Plant Layout: Fundamentals and Fine Points of Optimum Facility Design.
Dearborn, MI: Society of Manufacturing Engineers.
Raoot, A.D. & Rakshit, A. (1993). "A 'linguistic pattern' approach for
multiple criteria facility layout problems", International Journal of
Production Research, 31(1), 203-222. https://doi.org/10.1080/00207549308956721
Real, R., Pralus, M., Pillet,
M., & Guizzi, L. (2010). Une première étape vers le Lean dans les
entreprises de sous-traitance mécanique, retour sur 7 ans de pratique. Revue
Française De Gestion Industrielle, 29(1), 71–86. https://doi.org/10.53102/2010.29.01.619
Rouse, P. & Putterill, M. (2003). An integral framework for performance measurement. Management
Decision, 41(8), 791-805. https://doi.org/10.1108/00251740310496305
Sarker, B.R. & Xu, Y.
(2000). " Designing multi-product lines: job routing in cellular
manufacturing systems ", IIE Transactions. 32(3), 219-235. https://doi.org/10.1080/07408170008963894
Selim, H.M., Askin, R.G.,
Vakharia, A.J. (1998). "Cell formation in group technology: review,
evaluation and directions for future research", Computers &
Industrial Engineering, 34(1), 3-20. https://doi.org/10.1016/S0360-8352(97)00147-2
Singh, S.P & Sharma, R.R.K.
(2006). A review of different aproaches to the facility layout problem, The
International Journal of Advanced Manufacturing Technology, 30, 425-433. https://doi.org/10.1007/s00170-005-0087-9
Srinivasan, G., Narendran, T.T.
& Mahadevan, B. (1990). An assignment model for the part-families problem
in Group Technology. International Journal of Production Research,
28(1), 145–152. https://doi.org/10.1080/00207549008942689
Tompkins, J. A., White, J. A.,
Bozer, Y. A., & Tanchoco, J. M. A. (2010). Facilities planning. 4th Edition, John Wiley & Sons.
Yin, Y., & Yasuda, K.
(2006). Similarity coefficient methods applied to the
cell formation problem: A taxonomy and review. International Journal of
Production Economics, 101(2), 329–352. https://doi.org/10.1016/j.ijpe.2005.01.014
Zhou, J., & Irani S. A.
(2003). New flow diagramming scheme for mapping and
analysis of multi-product flows in facility. Journal of Integrated Design
and Process Science, 7(1), 25-58. https://content.iospress.com/articles/journal-of-integrated-design-and-process-science/jid7-1-03
Zhou J., Barth, M. & De Guio R. (1996). Quasi-source heuristic for the production line formation of
manufacturing system. IEEE International Conference on Systems, Man and
Cybernetics. Information Intelligence and Systems (Cat. No.96CH35929), 4, pp.
3009-3014. https://doi.org/10.1109/ICSMC.1996.561444.
9. BIOGRAPHIE
 David
Damand : est maître de conférences (HC) à l'EM Strasbourg (Université
de Strasbourg, France) et chercheur au laboratoire HUMANIS. Il enseigne la
planification de la chaîne logistique. Ses travaux portent sur l'analyse
décisionnelle multicritères pour la planification de la chaîne logistique et la
méthodologie de conception d'entrepôts.
David
Damand : est maître de conférences (HC) à l'EM Strasbourg (Université
de Strasbourg, France) et chercheur au laboratoire HUMANIS. Il enseigne la
planification de la chaîne logistique. Ses travaux portent sur l'analyse
décisionnelle multicritères pour la planification de la chaîne logistique et la
méthodologie de conception d'entrepôts.
 Marc
Barth : est maître de conférences habilité à diriger les recherches en
génie industriel à l'INSA de Strasbourg en France. Il est membre du laboratoire
de recherche HUMANIS de l'EM Strasbourg. Ses recherches et son enseignement
portent sur les applications de la planification et du contrôle de la
production, la théorie de la résolution de problèmes inventifs, l'application
des méthodes activity based costing et time driven activity based costing et la
conception des systèmes de production et des entrepôts.
Marc
Barth : est maître de conférences habilité à diriger les recherches en
génie industriel à l'INSA de Strasbourg en France. Il est membre du laboratoire
de recherche HUMANIS de l'EM Strasbourg. Ses recherches et son enseignement
portent sur les applications de la planification et du contrôle de la
production, la théorie de la résolution de problèmes inventifs, l'application
des méthodes activity based costing et time driven activity based costing et la
conception des systèmes de production et des entrepôts.
 Abdehlatif
Dhkil : est professeur associé en génie industriel à l’Ecole de
Technologie Supérieur - Département de génie de la production automatisée (Université
du Québec à Montreal, Canada) et chercheur au LIPPS (Laboratoire d’Ingénierie
des Produits, Procédés et Systèmes). Ses recherches portent sur la conception
de systèmes de production et la représentation de carte cognitives pour
l’analyse.
Abdehlatif
Dhkil : est professeur associé en génie industriel à l’Ecole de
Technologie Supérieur - Département de génie de la production automatisée (Université
du Québec à Montreal, Canada) et chercheur au LIPPS (Laboratoire d’Ingénierie
des Produits, Procédés et Systèmes). Ses recherches portent sur la conception
de systèmes de production et la représentation de carte cognitives pour
l’analyse.
